
Our research interests are in the development and analysis of approximation schemes for nonlinear partial differential equations arising in materials science and geometry. Investigated model problems include nonconvex energy minimization describing phase transitions in crystalline alloys allowing for microstructure formation, nonlinear geometric evolution problems for maps taking values in a given submanifold arising in liquid crystal theories, and phase field models described by singularly perturbed, semilinear parabolic partial differential equations modeling phase transitions in binary alloys. Employed theoretical techniques include relaxation theory leading to measure valued solutions, weak compactness results based on moving frames, and robust estimates on principal eigenvalues of linearized operators. Aspects in the development of approximation schemes range from mixed and nonconforming finite element methods and adaptive mesh refinement to finite elements on surfaces and stability of implicit and explicit discretizations. Specific areas are:
 |
 |
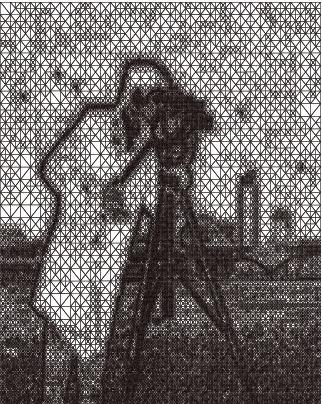 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
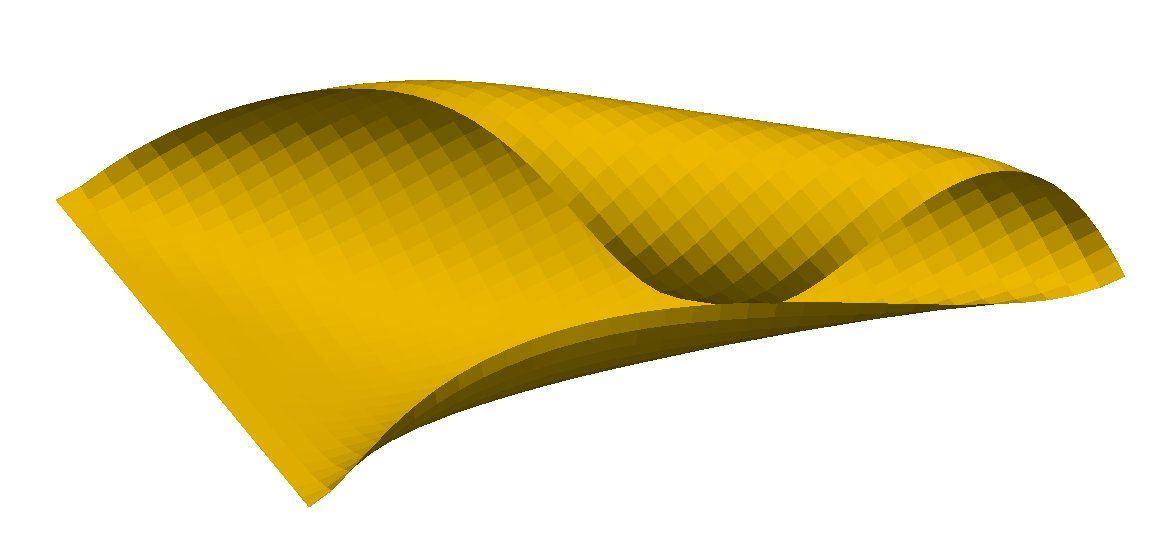
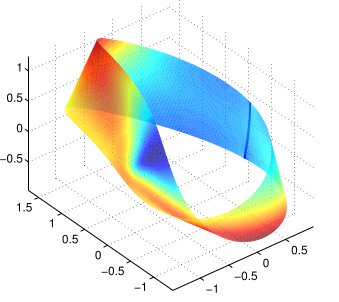
Thin elastic objects arise in various classical and modern applications, e.g., in the construction of lightweight curved roofs or fabrication of polymeric nanotubes. Effective mathematical descriptions eliminate the small thickness parameter via limit passages from general three-dimensional models to dimensionally reduced shell or rod models. When bending behavior dominates and shearing effects such as stretching or compression can be neglected the reduced shell model coincides with Kirchhoff's nonlinear bending model which seeks a deformation $y:\omega \to \mathbb{R}^3$ of the initially flat sheet $\omega$ that minimizes a bending energy subject to an isometry constraint, i.e., $$ E(y) = \frac{1}{12} \int_\omega |II|^2 ds, \quad I = {\rm id}, $$ with the first and second fundamental forms $I$ and $II$ of the surface parametrized by $y$. The fourth order nature of the model and the nonlinear constraint require the development of appropriate mixed or nonconforming finite element methods and stable iterative solution methods. The developed simulation techniques have applications in the prediction of the construction of nanotubes and microcapsules made of polymer bilayers. Current research aspects are the improvement of the efficiency of convergent methods and the development of schemes that guarantee injectivity.
 |
 |
Selected contributions
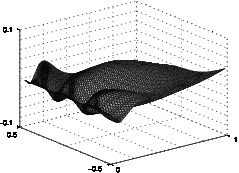
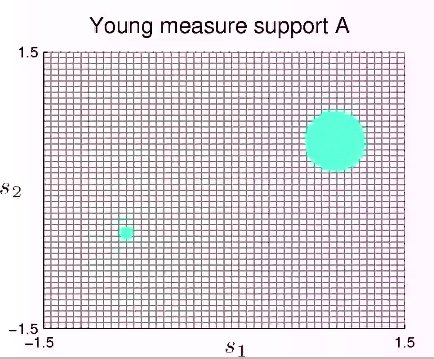
Plastic material behavior is a nonlinear process that occurs in the deformation of solids when the material ceases to respond elastically to applied forces. It is related to remaining microstructural changes in the crystalline lattice. Simple mathematical descriptions use concepts from convex analysis to model the threshold of elasticity and the compensation of forces exceeding this value, e.g., via $$ \partial_t p \in \partial I_K(\sigma), \quad - {\rm div} \big(\mathbb{C}\varepsilon(u)-p\big) = f $$ with a convex set $K$ of admissible elastic stresses and the subdifferential $\partial I_K$ of its indicator functional. Another microstructural process that influences the macroscopic mechanical behavior of a solid are crystalline phase transitions. These can be related to environmental changes such as temperature. The crystalline lattice then prefers different configurations leading to the formation of microstructure such as laminates or branching effects. Mathematical descriptions can be based on homogenization techniques that eliminate the microscale via certain averages or introduce an additional variable that locally describes the microstructure via families of probability measures called Young measures, e.g., $$ E(u,\mu) = \int_\Omega \int_{\mathbb{R}^{d\times d}} W(s) \, d \mu_x(s) - \int_\Omega f \cdot u \, d x, \quad \nabla u(x) = \int_{\mathbb{R}^{d\times d}} s \, d \mu_x(s). $$ A general framework for the mathematical modeling of microstructural phenomena taking place on slow time scales is provided by the concept of rate-independence.
 |
Selected contributions
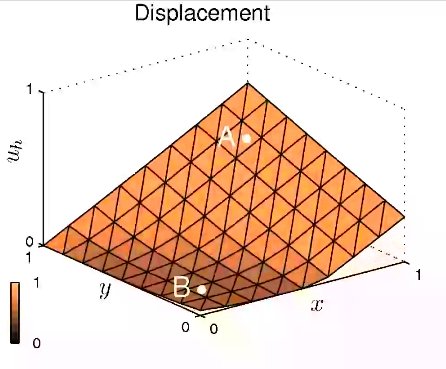
The mathmematical modeling of various real-world applications requires describing quantities that cannot be expected to be continuous and typically jump across lower-dimensional subsets. A concise mathematical framework is provided by functions of bounded variation which are classes of integrable functions whose distributional gradients define certain measures. A simple model problem that captures many important features is related to image processing and seeks for a given noisy image described by a gray-scale function $g:\Omega \to \mathbb{R}$ a regularized image $u:\Omega \to \mathbb{R}$ vai minimizing $$ E(u) = \int_\Omega |Du| + \frac{\alpha}{2} \|u-g\|_{L^2(\Omega)}^2, $$ where the first term is the total variation of the measure $Du$ and the second one penalizes deviations of $u$ from $g$. While convergence of $W^{1,1}(\Omega)$ conforming finite element methods is a straightforward consequence of appropriate density results, the derivation of convergence rates and the development of iterative schemes for the practical minimization are challenging tasks. Our research interests are related to the construction of weak interpolation operators and solution methods based on convex duality arguments.
 |
Selected contributions
Geometric partial differential equations refer to partial differential equations that are defined on a curved manifold or which prescribe a mapping that is constraint to attain its values in a given manifold. Such equations model diffusion processes on surfaces and the orientation of rod-ike liquid-crystal molecules. A prototypical partial differential equation defined on a surfaces is formulated via the Laplace-Beltrami operator via $$ \int_\Gamma \nabla_\Gamma u \cdot \nabla_\Gamma v \, ds = \int_\Gamma f v \, ds \ \, \forall v \quad \Longleftrightarrow \quad -\Delta_\Gamma u = f $$ where $\nabla_\Gamma u$ is the tangential component of the full gradient of an extension of $u$ to the ambient space. A prototypical manifold-constrained partial differential equation defines harmonic maps into unit spheres via $$ -\Delta u = |\nabla u|^2 u, \quad |u|^2 = 1. $$ Difficulties in the numerical solution of geometric partial differential equations are related to the approximation of the surface and the corresponding approximation of the differential operators as well as the effective discretization of nonlinear pointwise constraints. Our contributions range from convergence theories for harmonic maps into general classes of manifolds and the development of stable iterative schemes to the mathematical modeling of director fields on flexible surfaces.
Selected contributions
Localized features of solutions for partial differential equations such as interfaces or singularities lead to a suboptimal convergence behavior of numerical methods when uniform meshes are used. Adaptive methods refine the mesh locally and automatically adjust it to the special features of particular solutions. This often leads to quasioptimal convergence rates. The refinement process is typically based on a posteriori error estimates of the form $$ \|u-u_h\| \le c \Big(\sum_{T\in \mathcal{T}_h} \eta_T^2(u_h)\Big)^{1/2} $$ with a partition $\mathcal{T}_h$ of the computational domain and computable refinement indicators $\eta_T(u_h)$. Elements $T \in \mathcal{T}_h$ are refined if the associated refinement indicator exceeds a fraction of their average. While these concepts are well-established for linear elliptic partial differential equations, nonlinear and nonsmooth problems require new techniques. Based on spectral estimates and primal-dual gap techniques we develop a posteriori error estimates for phase-field and total-variation regularized problems. In the case of time-dependent problems locally refined meshes have to be coarsened when localized features have advanced in time which poses a challenging algorithmic problem.
Selected contributions
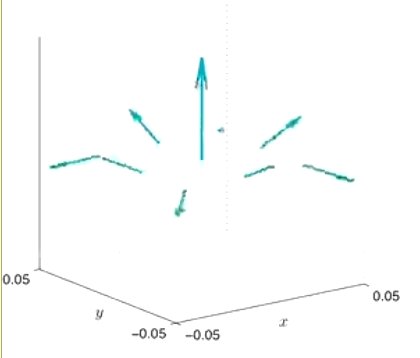
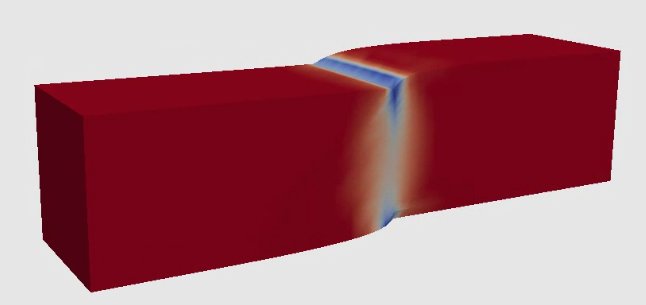
Phase-field models desribe physical processes in which the system can be locally at different states, e.g., a solid and liquid state in mixing and melting processes. The simplest example is the Allen-Cahn equation which determines a function $u$ via the semilinear partial differential parabolic equation $$ \partial_t u - \Delta u = - \varepsilon^{-2} f(u) $$ with a function $f$ that vanishes at the preferred states. The small parameter $\varepsilon>0$ determines the width of interfaces separating regions in different phases. The interfaces evolve in time and may undergo topological changes, e.g., when particles merge or disappear. Such phenomena are related to instabilities and large velocities which are difficult to approximate accurately. In particular, standard error estimates lead to an exponential dependence on the inverse of the phase-field parameter, e.g., $$ \|u-u_h\| \le c \exp(\varepsilon^{-2} T) \Phi(u,\tau,h), $$ which is of limited practial value. Improved estimates with an algebraic dependence on $\varepsilon^{-1}$ are obtained by incorporating precise localized stability information of the process provided by the principal eigenvalue of the linearized differential operator. A key observation is that the time-averaged eigenvalue grows logarithmically in $\varepsilon^{-1}$ and thus allows for the derivation of robust error estimates. Related important scientific questions include the treatment of singular potentials and degenerate equations.
Selected contributions